|
EN BREF
|
La trigonométrie est une branche des mathématiques essentielle qui explore les relations entre les angles et les côtés des triangles. Parmi les outils fondamentaux de cette discipline, le tableau trigonométrique occupe une place centrale. Il répertorie les valeurs cruciales des fonctions trigonométriques, telles que le sinus et le cosinus, facilitant ainsi le calcul des longueurs et des angles dans divers contextes. Grâce à ce tableau, les étudiants et les professionnels peuvent rapidement accéder aux informations dont ils ont besoin pour résoudre des problèmes complexes et d’appliquer les concepts trigonométriques à des situations pratiques. La compréhension de cet outil est donc primordiale pour quiconque souhaite maîtriser cette discipline fascinante.
Le tableau de trigonométrie constitue un outil essentiel pour quiconque souhaite appréhender les relations entre les angles et les longueurs dans le contexte de la trigonométrie. Ce manuel répertorie les valeurs des fonctions trigonométriques telles que le sinus, le cosinus et la tangente, facilitant ainsi les calculs complexes. Dans cet article, nous explorerons ses composantes, son utilisation pratique, et son importance dans les mathématiques et au-delà.
Les bases du tableau de trigonométrie
Le tableau de trigonométrie est un récapitulatif des valeurs des fonctions trigonométriques pour des angles particuliers. Il inclut généralement des angles standards comme 0°, 30°, 45°, 60° et 90°. Chacun de ces angles présente des valeurs de sin, cos, et tan qui sont fréquemment utilisées dans différents calculs.
La maîtrise de ces valeurs est fondamentale pour résoudre des problèmes géométriques simples, mais aussi pour des applications plus complexes en physique et en ingénierie. Un bon usage du tableau permet de gagner du temps et d’éviter des erreurs lors du calcul de grandeurs comme des distances ou des hauteurs.
Le cercle trigonométrique : une aide visuelle
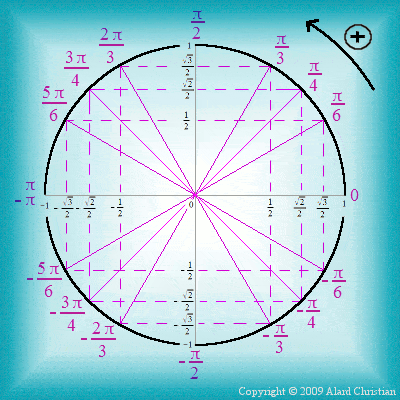
Pour mieux comprendre les valeurs répertoriées dans le tableau, il est primordial d’intégrer le concept du cercle trigonométrique. Ce cercle de rayon 1 permet de visualiser les relations entre les angles et les coordonnées des points qui le composent. En effet, chaque angle correspond à un point sur le cercle dont les coordonnées (x,y) représentent respectivement le cosinus et le sinus de cet angle.
Le cercle trigonométrique facilite également l’appréhension des angles négatifs et des angles supérieurs à 90°, ouvrant la voie à des calculs plus avancés. Ainsi, comprendre le tableau de trigonométrie s’accompagne souvent d’une bonne compréhension de cette aide visuelle.
Applications pratiques du tableau de trigonométrie
Les applications du tableau de trigonométrie sont vastes et se retrouvent dans de nombreux domaines. Par exemple, en architecture, il permet de calculer des pentes, des hauteurs ou des distances indirectes. En navigation, il aide à déterminer la position et le cap à suivre.
Dans le domaine de la physique, le tableau est utilisé pour résoudre des problèmes impliquant des forces, des vitesses et des trajectoires. La connaissance des valeurs spécifiques des fonctions trigonométriques facilite par ailleurs la compréhension des oscillations, des ondes et d’autres phénomènes périodiques.
L’importance de la pratique
Pour tirer le meilleur parti du tableau de trigonométrie, une pratique régulière est conseillée. Les exercices de calcul utilisant les valeurs du tableau, en relation avec des problèmes géométriques, renforcent la compréhension des concepts. Cela inclut des problèmes nécessitant le calcul de longueurs et d’angles inconnus.
En investissant du temps dans la familiarisation avec le tableau de trigonométrie et ses applications, toute personne intéressée par les mathématiques pourra en saisir toute la richesse et l’utilité dans ses études ou sa profession.
Outils et Applications de la Trigonométrie
| Outils | Applications |
| Cercle trigonométrique | Permet de visualiser les valeurs des fonctions sinus et cosinus pour tous les angles. |
| Tableau trigonométrique | Répertorie les valeurs remarquables des fonctions pour des angles spécifiques. |
| Formules trigonométriques | Utilisées pour calculer des longueurs et des angles dans les triangles. |
| Identités trigonométriques | Facilitent la simplification et la résolution de problèmes complexes. |
| Rapports trigonométriques | Aide à établir des relations entre les côtés et les angles des triangles. |
| Angles particuliers | Permettent des calculs rapides grâce à des valeurs prédéfinies. |
| Médiatrices et bissectrices | Utilisées pour des constructions géométriques précises et des calculs d’aires. |
| Fonctions inverses | Permettent le calcul des angles à partir des longueurs des côtés. |
| Applications pratiques | On les utilise dans divers domaines comme l’architecture, l’ingénierie et la physique. |
Le tableau de trigonométrie est un outil essentiel pour quiconque souhaite maîtriser les relations entre les angles et les côtés dans un triangle. En rassemblant des valeurs de sinus, cosinus et tangente, il permet de simplifier de nombreux calculs en trigonométrie. Cet article vous guide à travers les différentes composantes de ce tableau et explore ses applications pratiques dans le domaine des mathématiques.
Les composantes du tableau de trigonométrie
Un tableau de trigonométrie comprend principalement les valeurs de sinus et cosinus pour des angles spécifiques qui vont de 0 à 90 degrés. Ces valeurs sont souvent représentées sous forme de fractions, tout en incluant aussi leurs approximations décimales pour un usage simplifié. En comprenant ces valeurs, il devient plus facile de résoudre des problèmes liés aux angles dans les triangles.
L’importance des angles remarquables
Les angles remarquables tels que 0°, 30°, 45°, 60° et 90° ont des valeurs de sinus et cosinus qui sont faciles à retenir. Par exemple, pour 30°, le sinus est 1/2, tandis que le cosinus est √3/2. Ces valeurs particulières sont cruciales car elles permettent d’effectuer rapidement des calculs sans avoir besoin d’une calculatrice.
Applications pratiques du tableau de trigonométrie
Le tableau de trigonométrie s’applique dans diverses situations, notamment en géométrie et en physique. Par exemple, dans un triangle rectangle, il permet de déterminer les longueurs de côtés manquants en utilisant les relations trigonométriques. Il est également utilisé pour calculer des distances dans des problèmes impliquant des angles, ce qui est particulièrement utile en architecture et en ingénierie.
Utilisation dans la résolution d’équations
Lors de la résolution d’équations trigonométriques, le tableau devient un atout indispensable. Il permet d’identifier rapidement les valeurs des fonctions trigonométriques pour des angles donnés, simplifiant ainsi le processus de résolution d’équations et fournissant une base solide pour les calculs ultérieurs.
Maîtriser le tableau de trigonométrie pour des résultats optimaux
Pour tirer le meilleur parti de ce tableau, il est recommandé de s’entraîner à utiliser ces valeurs dans divers exercices. La pratique régulière aide à renforcer la compréhension et à rendre ces concepts plus accessibles. Que ce soit pour préparer un examen ou pour appliquer ces connaissances dans la vie quotidienne, maîtriser le tableau de trigonométrie est un atout inestimable.
- Tableau des valeurs de sinus
Répertorie les valeurs de sinus pour les angles courants.
- Tableau des valeurs de cosinus
Rassemble les valeurs de cosinus associées aux mêmes angles.
- Applications dans les triangles
Permet de calculer des longueurs et des angles dans les triangles.
- Utilisation avec le cercle trigonométrique
Facilite la compréhension des fonctions sinus et cosinus.
- Rappels de formules trigonométriques
Donne accès aux formules essentielles pour les calculs trigonométriques.
- Valeurs particulières
Identifie les angles usuels et leurs valeurs remarquables.
- Outils d’apprentissage
Propose des exercices pratiques pour maîtriser la trigonométrie.
- Applications pratiques
Utilisé en physique et en ingénierie pour résoudre des problèmes complexes.
Introduction au tableau de trigonométrie
Le tableau de trigonométrie, élément fondamental pour l’étude de cette discipline, récapitule les valeurs des fonctions essentielles telles que sinus et cosinus. Comprendre ce tableau permet de résoudre rapidement des problèmes liés aux angles et aux distances dans divers contextes. Cet article vous présentera les outils associés au tableau de trigonométrie, ainsi que ses nombreuses applications dans le domaine des mathématiques.
Fonctions trigonométriques : un aperçu
Les fonctions sinus et cosinus sont centrales en trigonométrie. En effet, elles relient les angles d’un triangle rectangle à la longueur de ses côtés. Par exemple, pour un angle donné, le sinus est défini comme le rapport entre la longueur du côté opposé à cet angle et la longueur de l’hypoténuse. De son côté, le cosinus correspond au rapport entre la longueur du côté adjacent à l’angle et celle de l’hypoténuse. Ces fonctions trouvent leur place dans le tableau trigonométrique, qui enregistre leurs valeurs pour différents angles.
Structure du tableau trigonométrique
Le tableau de trigonométrie est souvent organisé en fonction des angles, généralement de 0° à 360°. Pour chaque angle, il présente non seulement les valeurs de sinus et cosinus, mais aussi celles de la tangente, qui est le rapport entre le sinus et le cosinus. Ce tableau comporte également des angles remarquables tels que 0°, 30°, 45°, 60° et 90°, dont les valeurs sont souvent mémorisées pour faciliter les calculs. En maîtrisant la structure de ce tableau, on parvient à l’exploiter efficacement dans divers problèmes.
Utilisation du tableau trigonométrique dans les calculs
Utiliser le tableau de trigonométrie permet de gagner un temps précieux dans les calculs. Lorsqu’on doit déterminer les longueurs des côtés d’un triangle ou les mesures d’angles, il suffit de consulter le tableau pour obtenir rapidement les valeurs nécessaires. Par exemple, si l’on connaît l’angle d’un triangle ainsi que la longueur de l’hypoténuse, on peut facilement retrouver les longueurs des autres côtés à l’aide des relations sinus et cosinus.
Applications pratiques du tableau de trigonométrie
La trigonométrie, et par extension le tableau trigonométrique, trouve une multitude d’applications dans des domaines variés. Elle est notamment utilisée en physique pour résoudre des problèmes liés à des mouvements oscillatoires, en ingénierie pour calculer des forces et des angles, et même en astronomie pour évaluer des distances entre étoiles ou planètes. Dans le monde réel, par exemple, on peut s’en servir pour déterminer l’ombre d’un bâtiment en observant l’angle du soleil.
Exercices pour mieux maîtriser le tableau
Pour s’approprier le tableau trigonométrique, il est essentiel de pratiquer régulièrement. Des exercices simples peuvent consister à déterminer les valeurs de sinus, cosinus, et tangente pour des angles donnés, ou encore à résoudre des problèmes concrets requérant l’utilisation de ces valeurs. Par ailleurs, il est bénéfique d’explorer le cercle trigonométrique, qui illustre les relations entre les angles et les fonctions trigonométriques, permettant ainsi d’ancrer ces concepts de manière plus intuitive.